In terms of accurate time, three situations can occur at sea:

1. We know the accurate UTC time – everything is fine, we can use all available astronavigation methods
2. We have no time source – we are limited to measuring latitude by the following methods:
   1. Meridian passage of the celestial body (e.g. LAN sight of the Sun)
   2. Zenith passage of the celestial body
   3. Polaris measurement with estimated Q correction
3. We have a working clock, but we don’t know its error – We are essentially in a situation before the invention of the precise chronometer. Thanks to the ability to measure time intervals, we can use any of these methods:
   1. Latitude check using the method of equal heights (or iterative determination of latitude)
   2. Determining latitude from two sights
   3. Position (and time) by the method of lunar distances
   4. Iterative determination of clock error using the lunar altitude method
   5. Correction of clock error by taking sights at a known position
   6. Determining the position and clock error using eclipses and occultations (very rare)
   7. Clock error correction using the Galilean moons of Jupiter (difficult to use)

In the following text, we will discuss the methods we briefly outlined above in more detail.

Latitude From Meridian Passage

A classic method of determining latitude with a thousand-year history. All we need to do is measure the height of a celestial body above the horizon at its culmination and know its current declination.
The most commonly used celestial body is the Sun, so we call this method the local apparent noon (LAN) method. The disadvantage of the Sun is that its declination changes constantly, most rapidly around the equinoxes, when the declination changes by more than 20 angular minutes in 24 hours, and most slowly around the solstices, when it remains virtually unchanged for several days.
The altitude of stars and planets can usually only be measured during nautical dawn and dusk, which makes this method difficult to use.
Under certain conditions, it should be possible to use the culmination of the Moon, but this has not been tested in practice.

Latitude From Zenith Passage

A method known mainly from Polynesian navigation. It can be used at any time during the night and does not require a sextant. Extremely simple to calculate – when a star passes overhead, the observer’s latitude is equal to the star’s declination.
How can you tell when a star is directly overhead? That’s a topic for a separate article 🙂

Polaris Measurement With Estimated Q Correction

The North Star describes a circle around the North Magnetic Pole with a radius of approximately half an angular degree. If we want to measure latitude using the North Star, we must apply a correction Q, which represents the angular distance of the North Star from the pole at a given moment. If we do not have the exact time, we can estimate the correction using the current position of the circumpolar constellations (the Big Dipper, Cassiopeia). An excellent aid is this diagram created by Greg Rudzinski.

The three methods above work even if we don’t have any source of time. The following methods require us to be able to measure time intervals (stopwatch, watch that doesn’t show the exact time). We don’t need to have our time synchronized with UTC or know the current offset.

Latitude check using the method of equal heights

A very elegant method that we can use when we are unable to determine the height of an object using the true noon method. This happens surprisingly often on the ocean, even in tropical latitudes.
We need to measure how much time elapses between two moments when a celestial object (typically the Sun) is at the same height before and after culmination.
Then we ask ourselves: are we north or south of a certain latitude L?
We substitute the latitude we are checking into the formula

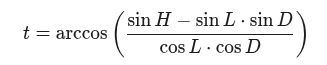
where H is the measured altitude of the celestial body and D is its declination.
Value t is the local hour angle of the body (LHA) at latitude L.
LHA represents the angle between the object and the local meridian, so when we multiply this value by two

we get the angle by which the Earth rotates during the time when the body is at the same height on its way up and on its way down.
We can directly convert this value to time in hours

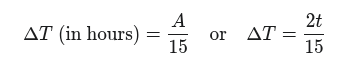
and compare it with the time we measured. If the calculated time is shorter than the measured time, it means that we are north of the checked latitude. If the calculated time is longer than the measured time, we are south of it. This applies if the declination and the checked latitude are in the same hemisphere (same name – summer); in winter, it will of course be the other way around.

Iterative Determination Of Latitude

We can repeat the above procedure for different latitudes and iteratively determine the actual latitude at which we are located.
If we use, for example, the bisection method, starting with a latitude that differs from our actual latitude by 3 degrees, we will achieve an accuracy better than 10 miles within five iterations.

Checking Latitude From Any Two Measurements

Of course, we can use the method of equal heights even if the measured heights are not equal, but this will double the number of calculations, because instead of one LHA calculation and multiplying by two, we have to calculate the LHA twice and subtract the angles from each other.
The rest of the procedure is the same, including the possibility of iterative determination of the actual latitude.

Position Using The Lunar Distance Method

The lunar distance method was the royal astronavigation discipline in the short period between the invention of the sextant (around 1760) and the deployment of usable chronometers (1770). It allows us to obtain both latitude and longitude. To use the method successfully, we need to take at least four measurements:

1. obtain local solar time using the local apparent noon method (LAN)
2. measure the Moon altitude
3. measure the altitude of the body whose lunar distance we will be measuring
4. measure the lunar distance

The last three measurements must be taken in a quick succession.
The method is very demanding in terms of measurement accuracy (especially lunar distance), requiring extensive tables and more calculations than other methods.
The Nautical Almanac publishes the tables needed for the calculations: https://thenauticalalmanac.com/Lunar_Distance_Tables.html
A brief (but sufficient) description of the method can be found here, for example: https://reednavigation.com/easylunars/
Using the lunar distance method, we are able to determine the longitude and can therefore correct the time on our clocks accordingly.

Iterative Determination Of Clock Error Using The Lunar Altitude Method

If we have a working clock but do not know its deviation from UTC, we can try to determine this deviation by measuring the altitude of the Moon. We do this by quickly measuring the altitude of two celestial bodies (preferably stars) and the altitude of the Moon. For practical use, the Moon needs to be as far east or west as possible.
In the next step, we will assume that the time on our watch is correct and calculate and plot three position lines obtained from the measurements.
The position lines will not intersect at a point but will form a triangle because the position line of the Moon will be subject to an error corresponding to the deviation of our watch from UTC due to its rapid movement across the sky. We will adjust the time, recalculate the position lines, and continue in this manner until we obtain the deviation of the watch with the required accuracy.
The entire procedure is described in detail here.
A potentially simpler calculation method (its functionality has not yet been verified) is to measure the altitude of the Sun and Moon twice during the day, calculate two sets of position lines, and determine the deviation of the clock as the difference in longitude between the intersections of these sets of position lines. The procedure is described here.

Correction of clock error by taking sights at a known position

If we are at a location whose geographical coordinates we know, we can determine the error of our clock quite easily. We will try to estimate the exact time (UTC) and perform a set of measurements. We will use the estimated time as if it were the actual time. The position lines of our measurements will intersect at a point that will be different from our current position. The deviation in latitude should be minimal (this is a check of our measurement), the deviation in longitude is directly proportional to the difference between the estimated time and the actual time – 4 time minutes for each geographical minute of longitude. If the intersection of the position lines is west of our actual position, our estimated time is ahead, if east, it is behind.




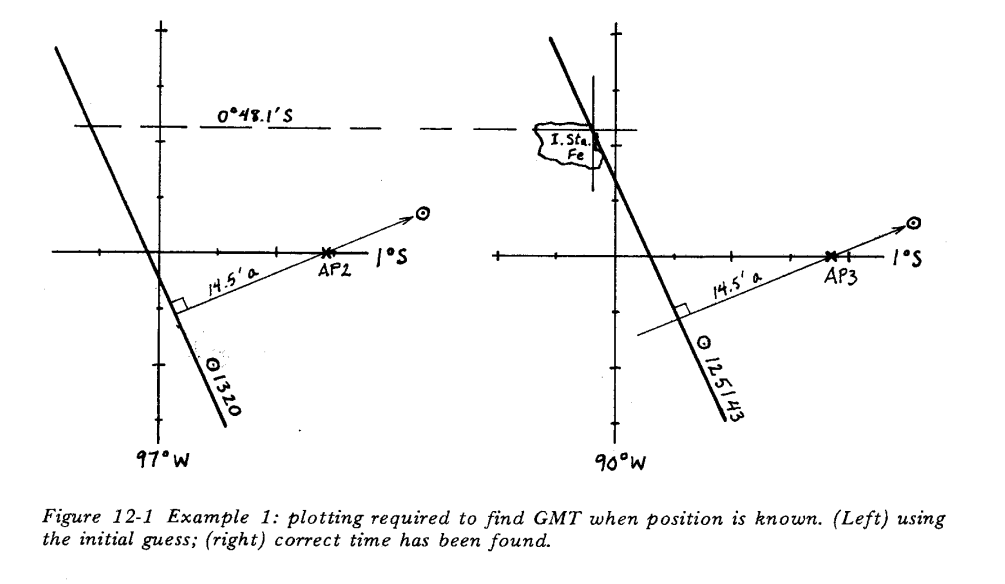
An example of clock correction from John Letcher’s excellent book Celestial Navigation with HO208.

Determining The Position And Clock Error Using Eclipses And Occultations (rare)

If the Earth were small enough, eclipses of the Sun and Moon or occultations of planets and other celestial bodies by the Sun or Moon would occur everywhere on Earth at the same moment, and if we counted down the time of their occurrence from local true noon (LAN), we would very easily obtain our longitude and thus UTC time.
In practice, however, the effect of parallax is quite large. This only makes the problem more complicated, not impossible. The longitude can be determined by an iterative process, but the rarity of eclipses and occultations and the computational complexity mean that if we want to label any celestial navigation method as interesting but very marginal, it will probably be this one.

Clock Error Correction Using The Galilean Moons Of Jupiter

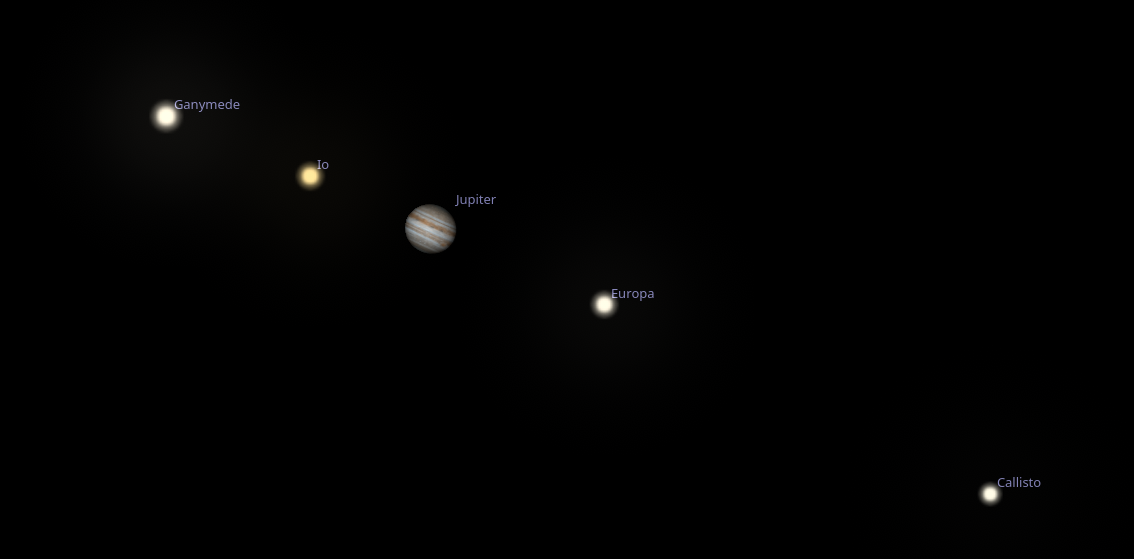
The orbits of Jupiter’s Galilean moons (Io, Europa, Ganymede, and Callisto) have only a slight inclination to the ecliptic plane and, when viewed from Earth (a pair of binoculars is usually sufficient), they lie almost in a straight line passing through Jupiter’s equator.
Their short orbital periods (tens to hundreds of hours) mean that they can be used as a dial to determine the exact time. This method have been used successfully on land to measure longitude, but it has never really caught on at sea. Perhaps it is time to return to it using modern technology and see if the moment has come for its renaissance.

Na první pohled je to jednoduchá úloha:
Předmět o výšce H vrhá stín o délce L. Jaký je v ten okamžik úhel, pod kterým vidíme Slunce vůči horizontu (na obrázku je označený jako e)?

Jedná se o pravoúhlý trojúhelník, kde známe dvě odvěsny (H a L) a hledáme přilehlý úhel, podle vzorce:

Takže úhel získáme obrácenou operací:

Pokud máme kalkulačku nebo matematické tabulky, je to skutečně velmi jednoduché.

Co když ale máme jen tužku a papír?

Až do 17. století bychom měli smůlu a hodnotu úhlu bychom nijak vypočítat nedokázali. Znamená to, že všichni slavní matematici minulosti ve starém Řecku, Arábii či Indii spoléhali na trigonometrické tabulky, které kdosi vytvořil tak, že skutečně fyzicky měřil rozměry na velké kružnici nakreslené na zemi.
Ještě Tycho de Brahe (1546-1601) si vytvářel vlastní tabulky, protože mu ty existující přišly málo přesné.

V 17. století několik matematiků nezávisle na sobě přišlo na to, že funkci arctan lze vyjádřit součtem nekonečné číselné řady

To zní dobře! Řada se snadno pamatuje (3,5,7, … střídání +/-) Stačí tedy vypočítat a sečíst dostatečné množství členů této řady a máme úhel. Pojďme se tedy podívat, kolik členů řady musíme sečíst, abychom dostali výsledek s přesností lepší než 10 úhlových minut, což je postačující pro hrubou astronavigaci.

Hm, začínají se objevovat problémy …

Pro malé úhly (do cca 30 stupňů) je počet členů, které je třeba sečíst pro dosažení požadované přesnosti, celkem malý (3-5 členů). Pak začíná prudce narůstat a pro 45 stupňů se limitně blíží nekonečnu. Pro úhly nad 45 stupňů řada diverguje, protože x je větší než jedna.

Tak jednoduché to tedy nebude. Nejprve se musíme vypořádat s úhly většími než 45 stupňů. Platí, že

Pro úhly nad 45 stupňů tedy budeme počítat s argumentem 1 / x a výsledek odečteme od 90 stupňů.

Pořád ale máme problém s raketovým nárůstem potřebných členů pro úhly blízké 45 stupňům. Odsud už žádná opravdu snadná cesta neexistuje, můžeme ovšem použít identitu, kterou objevil anglický matematik John Machin a která říká, že

To nám umožní rozdělit úhel na dva menší, které budou oba bezpečně pod 45 stupňů a řada nám pak bude snadněji konvergovat. Řekněme, že první argument zvolíme 0.5 (odpovídá úhlu cca 23 stupňů). Druhý argument pak vypočítáme podle vzorce

Pak vypočítáme arctan pro tuto hodnotu a pro 0.5 a oba výsledky sečteme. Není to úplně nejjednodušší cesta, ale stále se dle mého názoru pohybujeme na úrovni, která se dá zapamatovat a dá se vypočítat ručně.

Zde je tabulka s potřebným počtem členů a příslušnými transformacemi pro úhly od 10 do 80 stupňů.

Jak vidíte, převod délky stínu na úhel je docela netriviální záležitost, když nemáme k dispozici tabulky nebo kalkulačku. Proto bývaly na starých astrolábech vyryté pomocné trigonometrické stupnice a přesné tabulky se cenily zlatem.

S infomacemi, které máme dnes, si stačí zapamatovat jednu číselnou řadu a dvě transformace a převod lze během pár minut udělat jen s pomocí papíru a tužky.

Základem většiny astronavigačních metod je měření úhlové výšky Slunce (nebo jiného nebeského tělesa) nad obzorem. Obzorem (horizontem) se přitom myslí tečná rovina k povrchu Země na místě, kde se nacházíme.

Tečná rovina k povrchu Země v místě pozorovatele

Pokud se nacházíme na otevřeném moři, považujeme za aproximaci tečné roviny vodní hladinu kolem nás. Pro danou výšku našeho oka nad hladinou jsme schopni celkem přesně spočítat, jak daleko „vidíme“ a kde se tedy nachází náš horizont. Od výšky nebeského objektu, změřenou k tomuto horizontu, pak odečteme takzvaný dip, neboli úhlovou odchylku spojnice od oka k horizontu vůči mořské hladině.

$$\mathrm{dip}\approx \mathrm{1,76}\times \sqrt{\mathrm{výška\; oka\; nad\; hladinou\; [m]}}\mathrm{[\prime ]}$$

Dip závisí pouze na výšce oka nad hladinou, pohybuje se v řádu jednotek minut (pro výšku oka nad hladinou 3 metry jsou to cca 3 úhlové minuty) a v námořním almanachu bývá uveden i ve formě tabulky.

Nacházíme-li se na souši, je situace složitější. Kolem nás jsou kopce a údolí, stavby a stromy. To, co vidíme na horizontu, bývá v jiné nadmořské výšce, než místo, kde se nacházíme. Pro aproximaci tečné roviny horizontu proto používáme umělé pomůcky, jako například umělý horizont, nebo bublinkovou vodováhu v leteckém sextantu.

Tyto metody však mají řadu omezení. Umělý horizont nám zdvojnásobuje úhlovou výšku objektu, takže s ním nelze měřit tělesa, která se nacházejí vysoko na obloze. Jeho použití pro hvězdy v noci je obtížné. Bublinková vodováha v leteckých sextantech je nepřesná.
A pro mně osobně je měření vůči skutečnému horizontu jaksi „skutečnější“, přináší mi větší potěšení.

Nabízí se tedy otázka: potřebujeme na souši skutečně umělé pomůcky, nebo se (alespoň v některých případech) obejdeme bez nich?

Podívejme se ještě jednou na situaci, kdy se nacházíme na otevřeném moři. Stojíme na palubě plachetnice a pozorujeme horizont okolo nás. Jak daleko se tento horizont nachází? Jinými slovy, jak daleko vidíme, než se nám hladina skryje za obzor díky zakřivení Země?

Tečná rovina, skutečný horizont a horizont s překážkou

Vzdálenost horizontu od naší pozice, podobně jako dip, závisí pouze na výšce oka pozorovatele a lze ji vypočítat podle vzorce

$$\mathrm{vzdálenost\; horizontu}\approx \mathrm{2,08}\times \sqrt{\mathrm{výška\; oka\; nad\; hladinou\; [m]}}\mathrm{[NM]}$$

Řekněme, že se naše oko nachází ve výšce 2 metry nad vodní hladinou. Horizont je pak vzdálen cca 3 námořní mile. Vše, co je dál, se nám již skrývá za obzorem. Ve skutečnosti tedy nepotřebujeme být na otevřeném moři, abychom mohli používat k měření mořský horizont. Stačí nám, abychom ve směru měřeného objektu měli alespoň 3 námořní míle hladiny. Ostrovy, pevnina, či jiné objekty, které jsou dále ve stejném směru, nám nevadí, protože jejich základny jsou pod naším horizontem.

Tři námořní míle jsou asi pět a půl kilometru. I u nás najdeme vodní plochu, která má potřebnou rozlohu. Na Lipně můžeme bez obav měřit Slunce metodou pravého poledne z ostrůvku Tajvan proti vodní hladině, protože jižní břeh jezera je vzdálen téměř 6 kilometrů.

Místo pro měření Slunce metodou pravého poledne.

Pro nás, kteří žijeme na Severní Moravě, přichází v úvahu třeba Jezioro Goczałkowickie kousek za hranicemi v Polsku. V severojižním směru měří sice necelých 5 km, ale z východu na západ má přes 8,5 kilometru. V Rakousku není daleko Neusiedler See pod Vídní u maďarských hranic. Ideální jsou samozřejmě všechna velká Evropská jezera – Mazury, Balaton, Bodamské jezero, Ženevské jezero a podobně.

Jezioro Goczałkowickie

Co když máme v blízkosti větší vodní plochu, ale není dostatečně dlouhá na to, abychom na ní mohli pozorovat přirozený horizont? Znamená to, že jsme při měření odkázáni na umělé pomůcky? Naštestí ne. Pokud stojíme blízko hladiny a vodní plocha má alespoň kilometr na šířku, můžeme použít takzvaný dip short.

dip short

Už jsme si řekli, že při každém měření vůči horizontu tvořenému vodní hladinou musíme od změřené výšky odečíst dip. Je to proto, že naše oko není na stejné úrovni jako horizont, který je od nás vzdálen několik mil. Vzdálenost horizontu závisí pouze na na výšce oka pozorovatele a dip také. Co se však stane, pokud je břeh blíže, než přirozený horizont? Stále máme před sebou několik kilometrů rovné vodní hladiny. Pokud známe vzdálenost ku protějšímu břehu, můžeme celkem přesně vypočítat úhel našeho pohledu k linii břehu vůči tečné rovině horizontu.

Jinými slovy se dá říct, že dip je speciální případ dip short, ve kterém nepotřebujeme znát vzdálenost k horizontu, protože je přesně daná výškou pozorovatele a zakřivením Země.

Jak tedy vypočítáme dip short, když známe výšku oka pozorovatele a vzdálenost k protějšímu břehu? Zde je vzorec:

$\mathrm{dip\; short}\approx \mathrm{0,225}*d+\mathrm{3,435}*h/d\mathrm{[\prime ]}$

kde d je vzdálenost protějšího břehu v kilometrech a h je výška oka nad hladinou v metrech.

Popíšeme si teď průběh měření za použití dip short. Vybereme si vhodné místo na břehu jezera či vodní nádrže. Výšku nebeského objektu změříme vůči protějšímu břehu. Z mapy si zjistíme, jak daleko od nás protější břeh pod měřeným objektem je. Spočítáme dip short z výšky oka nad hladinou a vzdálenosti k protějšímu břehu. Použijeme jej pak stejně, jako bychom počítali s dipem na volném moři.

Velmi dobře to funguje například pro metodu pravého poledne, kdy měřený object (Slunce) je přesně na jih od nás, což nám zjednoduší měření vzdálenosti k protějšímu břehu na mapě.

Měření metodou pravého poledne na přehradě Olešná

Příklad: Měřím výšku Slunce nad horizontem metodou pravého poledne na přehradě Olešná. Stojím na severním břehu, oko mám 2 metry nad hladinou. Jižní břeh je ode mně vzdálen 1 kilometr. Dosazením do vzorce získám dip short 7 úhlových minut. Tuto hodnotu odečtu od meření, jako by to byl dip.

Protože astronavigátoři jsou zvyklí na tabulky a neradi počítají podle vzorců, připravil jsem přehlednou tabulku dip short pro běžné hodnoty výšky oka nad hladinou a vzdálenosti k protějšímu břehu. Ke stažení jsou zde: dipshort.pdf

Přeji přesná měření!

V čem vítězí Tatry?

Rozumná velikost. Všechny tatranské vrcholy jsou v dosahu jednodenní túry, za víkend se dají Tatry přejít křížem-krážem. Velmi to zjednodušuje logistiku a umožňuje poznat tyto krásné hory skutečně do hloubky. Navíc většina tatranských vrcholů je vlastně „na okraji“ hor a jsou z nich úžasné výhledy (za dobré viditelnosti jde z Tater vidět do pěti států najednou!)

Domluvíme se tam jazykem svého kmene. Návštěvníci Tater jsou převážně Slováci, Poláci a Češi, tedy národy, které jsou si jazykově a kulturně blízko. Což ocení zejména ten, kdo žil nějaký čas v zahraničí. Podobná kultura a mentalita usnadňují sdílení zážitků, o které na horách nikdy není nouze. Pokud by někdo na horské chatě v Alpách začal hrát na kytaru Hlídače krav od Nohavicy, budou na něj všichni koukat jako na zjevení. V Tatrách se brzy přidá celá chata (hlavně v refrénu)

A v čem vítězí Alpy?

Nástupy. V Alpách většinou vede asfaltová silnice až na konec údolí, tam je záchytné parkoviště a rovnou odtamtud začínají horské stezky. V Tatrách to takhle funguje snad jen na Zverovce, jinak je třeba zaparkovat daleko pod horami a pak nezáživně pochodovat dlouhé kilometry k nástupu stezek a uskakovat přitom autům, které mají to správné povolení.

Stezky a přístupnost. Alpy jsou protkány značenými stezkami. V podstatě platí, že pokud lze někam vést stezku, tak tam taky stezka je a může se po ní chodit. V létě, v zimě, jak je komu libo. Ne tak v Tatrách. Značené stezky vedou jen někam a jsou otevřené jen od jara do podzimu. Spousta míst – doliny i vrcholy – jsou pro běžného návštěvníka oficiálně nedostupné. Musíte mít buď správné kámoše (TANAP, horská služba), nebo zaplatit tučné výpalné a najmout si horského vůdce.
Typickým příkladem je Gerlachovský štít. V Alpách by na něj vedly minimálně dvě turistické stezky (z Batizovské a z Velické doliny), plus pár via ferrat. Gerlach je ale v Tatrách, takže značení tam není žádné (o to se starají horští vůdcové, kteří úmyslně rozkopávají mužíky) a abyste se mohli oficiálně projít na vrchol, musíte si buď za pár set euro najmout průvodce, nebo být členem nějakého horolezeckého spolku (a bloudit kamenolomem, protože chybí značení).

A je dobojováno. Jak to vidíte vy?

Mionší se prezentuje jako „největší jedlobukový prales Karpatského typu v ČR.“ Problém je, že tam nerostou jedle. A tak se správci rozhodli jít štěstíčku trochu naproti a semenáčky jedlí obalili pletivem. Když jedle, tak jedle.

Pletivem se v Mionší vůbec nešetří. Takových ohrad, kde je hodná příroda oddělená od zlé přírody tam lze nalézt několik.

V pralese jsou i stezky. Chodí po nich zvěř, správci, potentáti i zvědaví turisté. Přes stezku občas spadne strom. I nechce se znavenému ochranáři neustále přeskakovat padlý kmen. Vezme tedy motorovku a šmik – šmik, stezka je zase průchozí bez zaškobrtnutí.

Další zvláštností jsou louky. Kde by se v pralese vzaly louky? Copak by díky sukcesi za pár let nezarostly? A kdo je tam vlastně seče? Zřejmě skřítci pralesníčci je tam kosí za vlahých nocí, kdy je měsíc vysoko na obloze a kolem něj žluté kolo jako týden stará modřina.
Všimněte si také pletiva obehnaného kolem smrku.

Co s tou posekanou trávou? Skřítci pralesníčci jsou dosti unavení samotným sečením a tak kupky trávy prostě pohodí do lesa. Co oko nevidí, to srdce nebolí.

Kde je louka, tam musí být i posed. V tomto případě pralesní posed. Někdo by mohl namítnout, že je to určitě jen pozorovatelna, ale já vidím posed …

Romantické představy většinou utrpí při konfrontaci s realitou šrámy. Je bláhové čekat v hustě osídleném kraji skutečnou divočinu. Vždyť ta naše země (a to včetně pralesů) je jedna velká pěstěná zahrádka.

Ale abych nekončil na kyselou notu, tak přikládám také pár „pralesních“ fotek, které ukazují Mionší z té druhé, divočejčí stránky.

Jak jste na tom s astronomickými znalostmi? Dokážete se zorientovat na noční obloze a rozumíte základům nebeské mechaniky? Následující kvíz se sedmi otázkami vám pomůže zjistit, jak na tom jste.

1.

Jak starý je Měsíc na obrázku?

7 dní
17 dní
27 dní

2.

Na obrázku jsou:

Kuřátka
Slepičky
Kohoutci

3.

Kde můžete takto vidět oblohu?

Na severu Norska
Ve Španělsku
V Etiopii

4.

 

Kolik času uplynulo mezi těmito dvěma snímky?

1 hodina
3 hodiny
6 hodin

5. Pozorujete hvězdy v Kardašově Řečici. Je jasno. Za celou noc nespatříte Sirius, Orion, ani Plejády. Jaké je datum?

1. března
1. června
1. září

6. Můžete na obloze vidět zároveň Slunce a Měsíc v úplňku?

Za určitých okolností ano
Ne
Pouze na rovníku okolo jarní rovnodennosti

7.

Jak se nazývá mlhovina na obrázku?

Mlhovina Orionu
Mlhovina Andromedy
Krabí mlhovina

Skóre =
Správné odpovědi:

Dárek pro Martina, kterého ve skoro sedmi letech už nebaví sedět na miminkovské sedačce. Břicho sedavce je uzamykatelné a slouží jako schránka na cennosti.