Základem většiny astronavigačních metod je měření úhlové výšky Slunce (nebo jiného nebeského tělesa) nad obzorem. Obzorem (horizontem) se přitom myslí tečná rovina k povrchu Země na místě, kde se nacházíme.

Tečná rovina k povrchu Země v místě pozorovatele

Pokud se nacházíme na otevřeném moři, považujeme za aproximaci tečné roviny vodní hladinu kolem nás. Pro danou výšku našeho oka nad hladinou jsme schopni celkem přesně spočítat, jak daleko „vidíme“ a kde se tedy nachází náš horizont. Od výšky nebeského objektu, změřenou k tomuto horizontu, pak odečteme takzvaný dip, neboli úhlovou odchylku spojnice od oka k horizontu vůči mořské hladině.

$$\mathrm{dip}\approx \mathrm{1,76}\times \sqrt{\mathrm{výška\; oka\; nad\; hladinou\; [m]}}\mathrm{[\prime ]}$$

Dip závisí pouze na výšce oka nad hladinou, pohybuje se v řádu jednotek minut (pro výšku oka nad hladinou 3 metry jsou to cca 3 úhlové minuty) a v námořním almanachu bývá uveden i ve formě tabulky.

Nacházíme-li se na souši, je situace složitější. Kolem nás jsou kopce a údolí, stavby a stromy. To, co vidíme na horizontu, bývá v jiné nadmořské výšce, než místo, kde se nacházíme. Pro aproximaci tečné roviny horizontu proto používáme umělé pomůcky, jako například umělý horizont, nebo bublinkovou vodováhu v leteckém sextantu.

Tyto metody však mají řadu omezení. Umělý horizont nám zdvojnásobuje úhlovou výšku objektu, takže s ním nelze měřit tělesa, která se nacházejí vysoko na obloze. Jeho použití pro hvězdy v noci je obtížné. Bublinková vodováha v leteckých sextantech je nepřesná.
A pro mně osobně je měření vůči skutečnému horizontu jaksi „skutečnější“, přináší mi větší potěšení.

Nabízí se tedy otázka: potřebujeme na souši skutečně umělé pomůcky, nebo se (alespoň v některých případech) obejdeme bez nich?

Podívejme se ještě jednou na situaci, kdy se nacházíme na otevřeném moři. Stojíme na palubě plachetnice a pozorujeme horizont okolo nás. Jak daleko se tento horizont nachází? Jinými slovy, jak daleko vidíme, než se nám hladina skryje za obzor díky zakřivení Země?

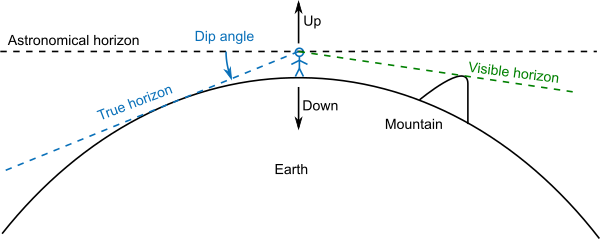
Tečná rovina, skutečný horizont a horizont s překážkou

Vzdálenost horizontu od naší pozice, podobně jako dip, závisí pouze na výšce oka pozorovatele a lze ji vypočítat podle vzorce

$$\mathrm{vzdálenost\; horizontu}\approx \mathrm{2,08}\times \sqrt{\mathrm{výška\; oka\; nad\; hladinou\; [m]}}\mathrm{[NM]}$$

Řekněme, že se naše oko nachází ve výšce 2 metry nad vodní hladinou. Horizont je pak vzdálen cca 3 námořní mile. Vše, co je dál, se nám již skrývá za obzorem. Ve skutečnosti tedy nepotřebujeme být na otevřeném moři, abychom mohli používat k měření mořský horizont. Stačí nám, abychom ve směru měřeného objektu měli alespoň 3 námořní míle hladiny. Ostrovy, pevnina, či jiné objekty, které jsou dále ve stejném směru, nám nevadí, protože jejich základny jsou pod naším horizontem.

Tři námořní míle jsou asi pět a půl kilometru. I u nás najdeme vodní plochu, která má potřebnou rozlohu. Na Lipně můžeme bez obav měřit Slunce metodou pravého poledne z ostrůvku Tajvan proti vodní hladině, protože jižní břeh jezera je vzdálen téměř 6 kilometrů.

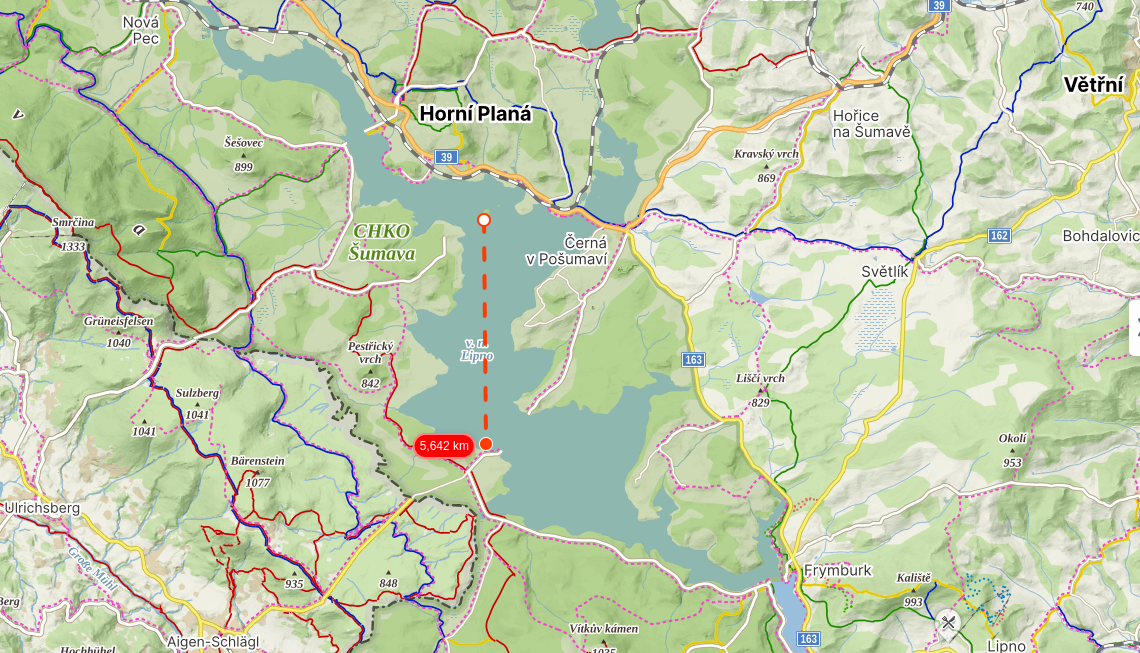
Místo pro měření Slunce metodou pravého poledne.

Pro nás, kteří žijeme na Severní Moravě, přichází v úvahu třeba Jezioro Goczałkowickie kousek za hranicemi v Polsku. V severojižním směru měří sice necelých 5 km, ale z východu na západ má přes 8,5 kilometru. V Rakousku není daleko Neusiedler See pod Vídní u maďarských hranic. Ideální jsou samozřejmě všechna velká Evropská jezera – Mazury, Balaton, Bodamské jezero, Ženevské jezero a podobně.

Jezioro Goczałkowickie

Co když máme v blízkosti větší vodní plochu, ale není dostatečně dlouhá na to, abychom na ní mohli pozorovat přirozený horizont? Znamená to, že jsme při měření odkázáni na umělé pomůcky? Naštestí ne. Pokud stojíme blízko hladiny a vodní plocha má alespoň kilometr na šířku, můžeme použít takzvaný dip short.

dip short

Už jsme si řekli, že při každém měření vůči horizontu tvořenému vodní hladinou musíme od změřené výšky odečíst dip. Je to proto, že naše oko není na stejné úrovni jako horizont, který je od nás vzdálen několik mil. Vzdálenost horizontu závisí pouze na na výšce oka pozorovatele a dip také. Co se však stane, pokud je břeh blíže, než přirozený horizont? Stále máme před sebou několik kilometrů rovné vodní hladiny. Pokud známe vzdálenost ku protějšímu břehu, můžeme celkem přesně vypočítat úhel našeho pohledu k linii břehu vůči tečné rovině horizontu.

Jinými slovy se dá říct, že dip je speciální případ dip short, ve kterém nepotřebujeme znát vzdálenost k horizontu, protože je přesně daná výškou pozorovatele a zakřivením Země.

Jak tedy vypočítáme dip short, když známe výšku oka pozorovatele a vzdálenost k protějšímu břehu? Zde je vzorec:

$\mathrm{dip\; short}\approx \mathrm{0,225}*d+\mathrm{3,435}*h/d\mathrm{[\prime ]}$

kde d je vzdálenost protějšího břehu v kilometrech a h je výška oka nad hladinou v metrech.

Popíšeme si teď průběh měření za použití dip short. Vybereme si vhodné místo na břehu jezera či vodní nádrže. Výšku nebeského objektu změříme vůči protějšímu břehu. Z mapy si zjistíme, jak daleko od nás protější břeh pod měřeným objektem je. Spočítáme dip short z výšky oka nad hladinou a vzdálenosti k protějšímu břehu. Použijeme jej pak stejně, jako bychom počítali s dipem na volném moři.

Velmi dobře to funguje například pro metodu pravého poledne, kdy měřený object (Slunce) je přesně na jih od nás, což nám zjednoduší měření vzdálenosti k protějšímu břehu na mapě.

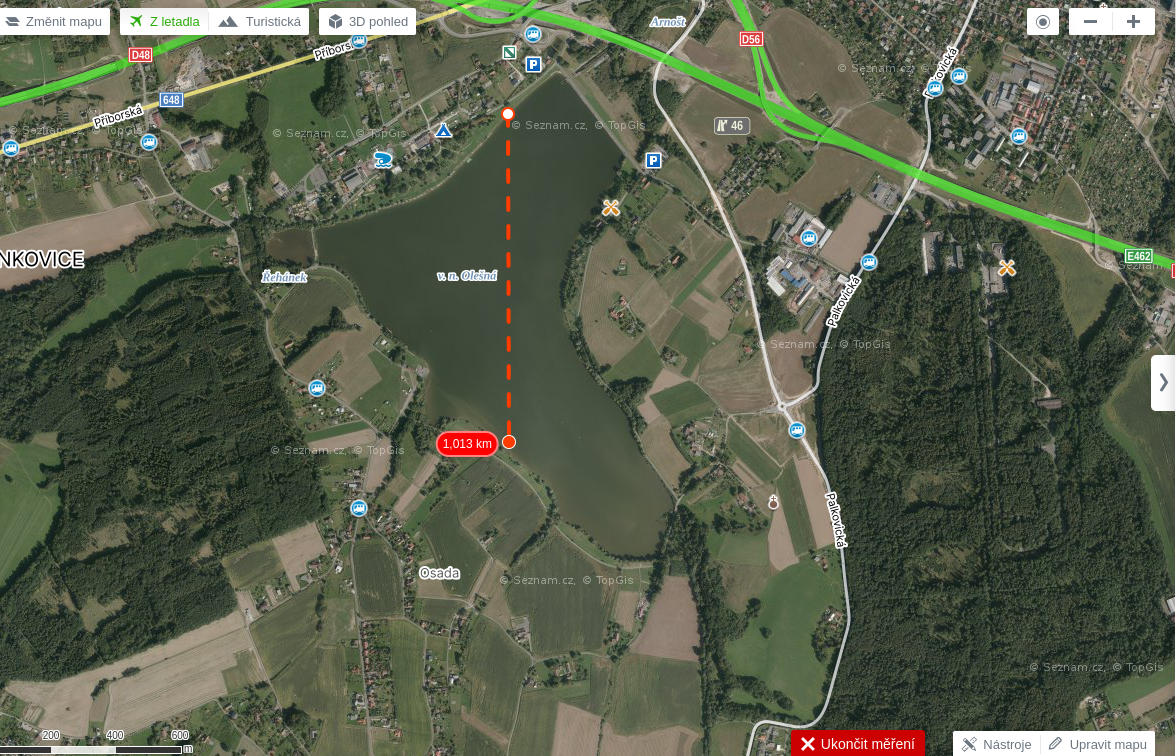
Měření metodou pravého poledne na přehradě Olešná

Příklad: Měřím výšku Slunce nad horizontem metodou pravého poledne na přehradě Olešná. Stojím na severním břehu, oko mám 2 metry nad hladinou. Jižní břeh je ode mně vzdálen 1 kilometr. Dosazením do vzorce získám dip short 7 úhlových minut. Tuto hodnotu odečtu od meření, jako by to byl dip.

Protože astronavigátoři jsou zvyklí na tabulky a neradi počítají podle vzorců, připravil jsem přehlednou tabulku dip short pro běžné hodnoty výšky oka nad hladinou a vzdálenosti k protějšímu břehu. Ke stažení jsou zde: dipshort.pdf

Přeji přesná měření!