Na první pohled je to jednoduchá úloha:
Předmět o výšce H vrhá stín o délce L. Jaký je v ten okamžik úhel, pod kterým vidíme Slunce vůči horizontu (na obrázku je označený jako e)?

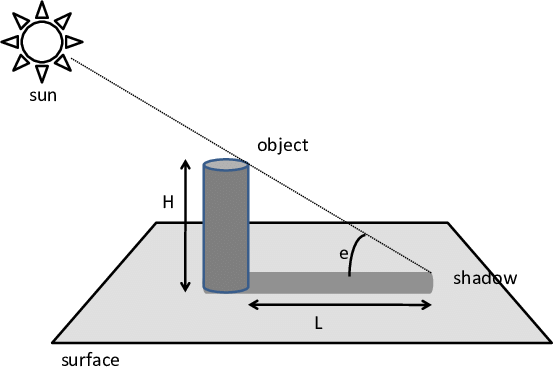
Jedná se o pravoúhlý trojúhelník, kde známe dvě odvěsny (H a L) a hledáme přilehlý úhel, podle vzorce:

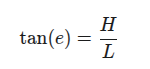
Takže úhel získáme obrácenou operací:

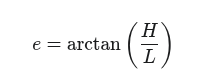
Pokud máme kalkulačku nebo matematické tabulky, je to skutečně velmi jednoduché.

Co když ale máme jen tužku a papír?

Až do 17. století bychom měli smůlu a hodnotu úhlu bychom nijak vypočítat nedokázali. Znamená to, že všichni slavní matematici minulosti ve starém Řecku, Arábii či Indii spoléhali na trigonometrické tabulky, které kdosi vytvořil tak, že skutečně fyzicky měřil rozměry na velké kružnici nakreslené na zemi.
Ještě Tycho de Brahe (1546-1601) si vytvářel vlastní tabulky, protože mu ty existující přišly málo přesné.

V 17. století několik matematiků nezávisle na sobě přišlo na to, že funkci arctan lze vyjádřit součtem nekonečné číselné řady

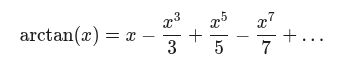
To zní dobře! Řada se snadno pamatuje (3,5,7, … střídání +/-) Stačí tedy vypočítat a sečíst dostatečné množství členů této řady a máme úhel. Pojďme se tedy podívat, kolik členů řady musíme sečíst, abychom dostali výsledek s přesností lepší než 10 úhlových minut, což je postačující pro hrubou astronavigaci.

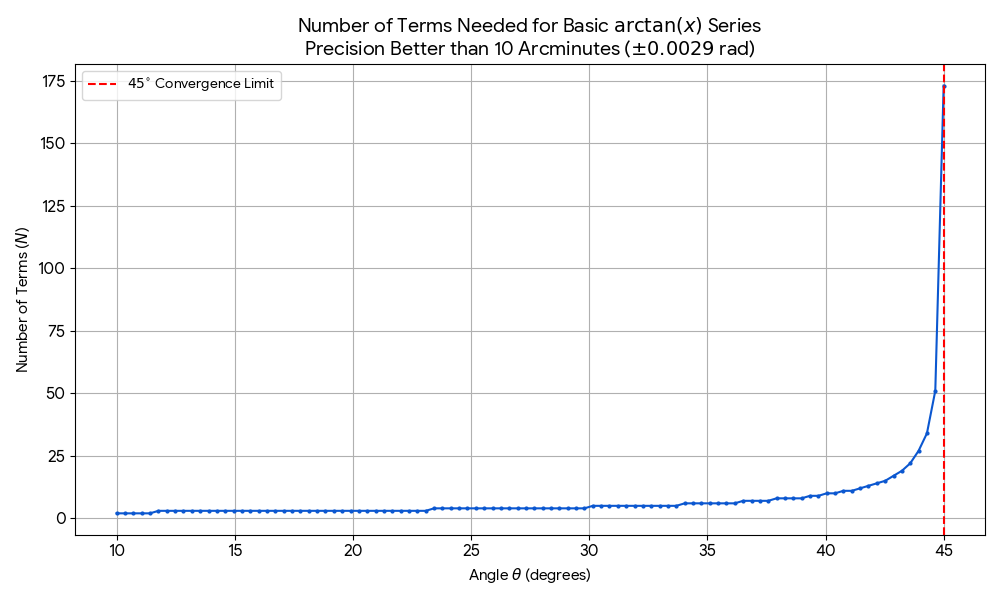
Hm, začínají se objevovat problémy …

Pro malé úhly (do cca 30 stupňů) je počet členů, které je třeba sečíst pro dosažení požadované přesnosti, celkem malý (3-5 členů). Pak začíná prudce narůstat a pro 45 stupňů se limitně blíží nekonečnu. Pro úhly nad 45 stupňů řada diverguje, protože x je větší než jedna.

Tak jednoduché to tedy nebude. Nejprve se musíme vypořádat s úhly většími než 45 stupňů. Platí, že

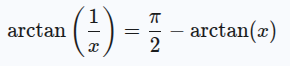
Pro úhly nad 45 stupňů tedy budeme počítat s argumentem 1 / x a výsledek odečteme od 90 stupňů.

Pořád ale máme problém s raketovým nárůstem potřebných členů pro úhly blízké 45 stupňům. Odsud už žádná opravdu snadná cesta neexistuje, můžeme ovšem použít identitu, kterou objevil anglický matematik John Machin a která říká, že

To nám umožní rozdělit úhel na dva menší, které budou oba bezpečně pod 45 stupňů a řada nám pak bude snadněji konvergovat. Řekněme, že první argument zvolíme 0.5 (odpovídá úhlu cca 23 stupňů). Druhý argument pak vypočítáme podle vzorce

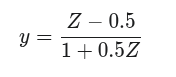
Pak vypočítáme arctan pro tuto hodnotu a pro 0.5 a oba výsledky sečteme. Není to úplně nejjednodušší cesta, ale stále se dle mého názoru pohybujeme na úrovni, která se dá zapamatovat a dá se vypočítat ručně.

Zde je tabulka s potřebným počtem členů a příslušnými transformacemi pro úhly od 10 do 80 stupňů.

Jak vidíte, převod délky stínu na úhel je docela netriviální záležitost, když nemáme k dispozici tabulky nebo kalkulačku. Proto bývaly na starých astrolábech vyryté pomocné trigonometrické stupnice a přesné tabulky se cenily zlatem.

S infomacemi, které máme dnes, si stačí zapamatovat jednu číselnou řadu a dvě transformace a převod lze během pár minut udělat jen s pomocí papíru a tužky.