In terms of accurate time, three situations can occur at sea:

1. We know the accurate UTC time – everything is fine, we can use all available astronavigation methods
2. We have no time source – we are limited to measuring latitude by the following methods:
   1. Meridian passage of the celestial body (e.g. LAN sight of the Sun)
   2. Zenith passage of the celestial body
   3. Polaris measurement with estimated Q correction
3. We have a working clock, but we don’t know its error – We are essentially in a situation before the invention of the precise chronometer. Thanks to the ability to measure time intervals, we can use any of these methods:
   1. Latitude check using the method of equal heights (or iterative determination of latitude)
   2. Determining latitude from two sights
   3. Position (and time) by the method of lunar distances
   4. Iterative determination of clock error using the lunar altitude method
   5. Correction of clock error by taking sights at a known position
   6. Determining the position and clock error using eclipses and occultations (very rare)
   7. Clock error correction using the Galilean moons of Jupiter (difficult to use)

In the following text, we will discuss the methods we briefly outlined above in more detail.

Latitude From Meridian Passage

A classic method of determining latitude with a thousand-year history. All we need to do is measure the height of a celestial body above the horizon at its culmination and know its current declination.
The most commonly used celestial body is the Sun, so we call this method the local apparent noon (LAN) method. The disadvantage of the Sun is that its declination changes constantly, most rapidly around the equinoxes, when the declination changes by more than 20 angular minutes in 24 hours, and most slowly around the solstices, when it remains virtually unchanged for several days.
The altitude of stars and planets can usually only be measured during nautical dawn and dusk, which makes this method difficult to use.
Under certain conditions, it should be possible to use the culmination of the Moon, but this has not been tested in practice.

Latitude From Zenith Passage

A method known mainly from Polynesian navigation. It can be used at any time during the night and does not require a sextant. Extremely simple to calculate – when a star passes overhead, the observer’s latitude is equal to the star’s declination.
How can you tell when a star is directly overhead? That’s a topic for a separate article 🙂

Polaris Measurement With Estimated Q Correction

The North Star describes a circle around the North Magnetic Pole with a radius of approximately half an angular degree. If we want to measure latitude using the North Star, we must apply a correction Q, which represents the angular distance of the North Star from the pole at a given moment. If we do not have the exact time, we can estimate the correction using the current position of the circumpolar constellations (the Big Dipper, Cassiopeia). An excellent aid is this diagram created by Greg Rudzinski.

The three methods above work even if we don’t have any source of time. The following methods require us to be able to measure time intervals (stopwatch, watch that doesn’t show the exact time). We don’t need to have our time synchronized with UTC or know the current offset.

Latitude check using the method of equal heights

A very elegant method that we can use when we are unable to determine the height of an object using the true noon method. This happens surprisingly often on the ocean, even in tropical latitudes.
We need to measure how much time elapses between two moments when a celestial object (typically the Sun) is at the same height before and after culmination.
Then we ask ourselves: are we north or south of a certain latitude L?
We substitute the latitude we are checking into the formula

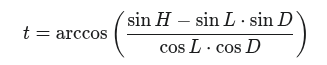
where H is the measured altitude of the celestial body and D is its declination.
Value t is the local hour angle of the body (LHA) at latitude L.
LHA represents the angle between the object and the local meridian, so when we multiply this value by two

we get the angle by which the Earth rotates during the time when the body is at the same height on its way up and on its way down.
We can directly convert this value to time in hours

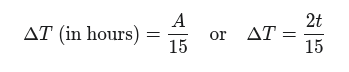
and compare it with the time we measured. If the calculated time is shorter than the measured time, it means that we are north of the checked latitude. If the calculated time is longer than the measured time, we are south of it. This applies if the declination and the checked latitude are in the same hemisphere (same name – summer); in winter, it will of course be the other way around.

Iterative Determination Of Latitude

We can repeat the above procedure for different latitudes and iteratively determine the actual latitude at which we are located.
If we use, for example, the bisection method, starting with a latitude that differs from our actual latitude by 3 degrees, we will achieve an accuracy better than 10 miles within five iterations.

Checking Latitude From Any Two Measurements

Of course, we can use the method of equal heights even if the measured heights are not equal, but this will double the number of calculations, because instead of one LHA calculation and multiplying by two, we have to calculate the LHA twice and subtract the angles from each other.
The rest of the procedure is the same, including the possibility of iterative determination of the actual latitude.

Position Using The Lunar Distance Method

The lunar distance method was the royal astronavigation discipline in the short period between the invention of the sextant (around 1760) and the deployment of usable chronometers (1770). It allows us to obtain both latitude and longitude. To use the method successfully, we need to take at least four measurements:

1. obtain local solar time using the local apparent noon method (LAN)
2. measure the Moon altitude
3. measure the altitude of the body whose lunar distance we will be measuring
4. measure the lunar distance

The last three measurements must be taken very quickly after each other.
The method is very demanding in terms of measurement accuracy (especially lunar distance), requiring extensive tables and more calculations than other methods.
The Nautical Almanac publishes the tables needed for the calculations: https://thenauticalalmanac.com/Lunar_Distance_Tables.html
A brief (but sufficient) description of the method can be found here, for example: https://reednavigation.com/easylunars/
Using the lunar distance method, we are able to determine the longitude and can therefore correct the time on our clocks accordingly.

Iterative Determination Of Clock Error Using The Lunar Altitude Method

If we have a working clock but do not know its deviation from UTC, we can try to determine this deviation by measuring the altitude of the Moon. We do this by quickly measuring the altitude of two celestial bodies (preferably stars) and the altitude of the Moon. For practical use, the Moon needs to be as far east or west as possible.
In the next step, we will assume that the time on our watch is correct and calculate and plot three position lines obtained from the measurements.
The position lines will not intersect at a point but will form a triangle because the position line of the Moon will be subject to an error corresponding to the deviation of our watch from UTC due to its rapid movement across the sky. We will adjust the time, recalculate the position lines, and continue in this manner until we obtain the deviation of the watch with the required accuracy.
The entire procedure is described in detail here.
A potentially simpler calculation method (its functionality has not yet been verified) is to measure the altitude of the Sun and Moon twice during the day, calculate two sets of position lines, and determine the deviation of the clock as the difference in longitude between the intersections of these sets of position lines. The procedure is described here.

Correction of clock error by taking sights at a known position

If we are at a location whose geographical coordinates we know, we can determine the error of our clock quite easily. We will try to estimate the exact time (UTC) and perform a set of measurements. We will use the estimated time as if it were the actual time. The position lines of our measurements will intersect at a point that will be different from our current position. The deviation in latitude should be minimal (this is a check of our measurement), the deviation in longitude is directly proportional to the difference between the estimated time and the actual time – 4 time minutes for each geographical minute of longitude. If the intersection of the position lines is west of our actual position, our estimated time is ahead, if east, it is behind.




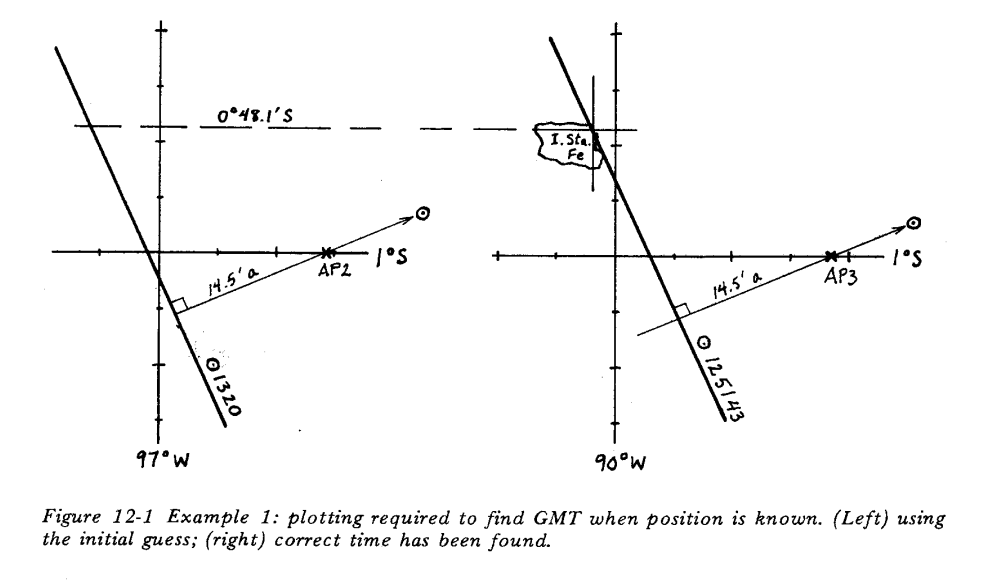
An example of clock correction from John Letcher’s excellent book Celestial Navigation with HO208.

Determining The Position And Clock Error Using Eclipses And Occultations (rare)

If the Earth were small enough, eclipses of the Sun and Moon or occultations of planets and other celestial bodies by the Sun or Moon would occur everywhere on Earth at the same moment, and if we counted down the time of their occurrence from local true noon (LAN), we would very easily obtain our longitude and thus UTC time.
In practice, however, the effect of parallax is quite large. This only makes the problem more complicated, not impossible. The longitude can be determined by an iterative process, but the rarity of eclipses and occultations and the computational complexity mean that if we want to label any astronavigation method as interesting but very marginal, it will probably be this one.

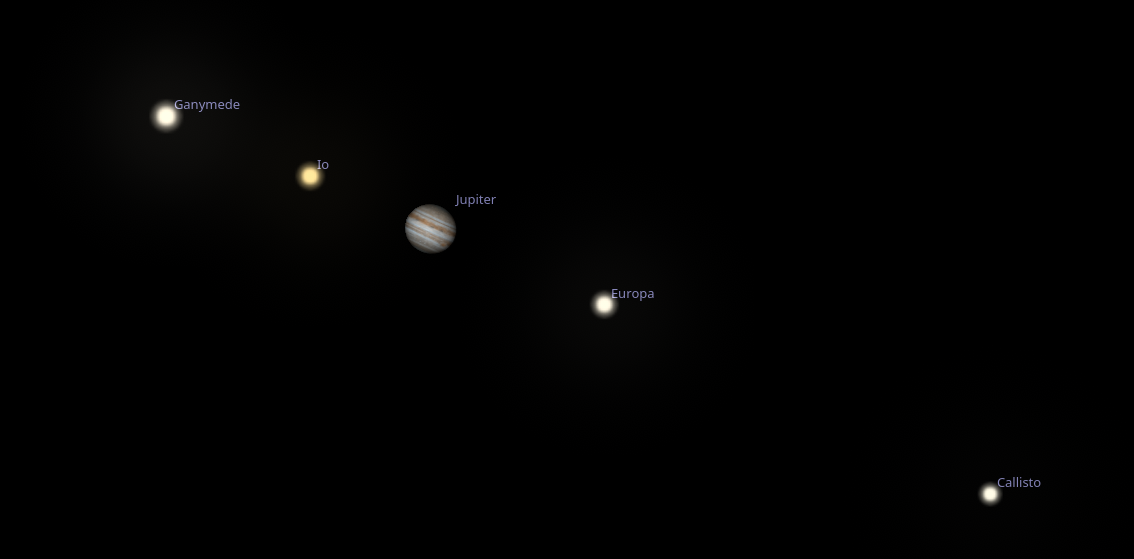
Clock Error Correction Using The Galilean Moons Of Jupiter

The orbits of Jupiter’s Galilean moons (Io, Europa, Ganymede, and Callisto) have only a slight inclination to the ecliptic plane and, when viewed from Earth (a pair pair of binoculars is usually sufficient), they lie almost in a straight line passing through Jupiter’s equator.
Their short orbital periods (tens to hundreds of hours) mean that they can be used as a dial to determine the exact time. They have been used successfully on land to measure longitude, but this method has never caught on at sea. Perhaps it is time to return to it using modern technology and see if the moment has come for its renaissance.