Z hlediska přesného času mohou na moři nastat tři situace:

1. Máme přesný čas – vše je v pořádku, můžeme používat všechny dostupné astronavigační metody
2. Nemáme žádný zdroj času – jsme omezeni na měření zeměpisné šířky následujícími metodami:
   1. průchod nebeského tělesa meridiánem (např. pravé poledne u Slunce)
   2. průchod nebeského tělesa nadhlavníkem
   3. měření Polárky s odhadem korekce Q
3. Máme funkční hodiny, ale neznáme jejich odchylku – nacházíme se v podstatě v situaci před vynálezem přesného chronometru. Díky tomu, že můžeme měřit časové intervaly, nabízí se nám tyto dodatečné možnosti:
   1. kontrola zeměpisné šířky metodou stejných výšek (případně iterativní určení zem. šířky)
   2. určení zeměpisné šířky ze dvou měření
   3. určení polohy (a času) metodou lunárních vzdáleností
   4. iterativní zjištení chyby hodin metodou lunární výšky
   5. korekce chyby hodin metodou lunárních vzdáleností
   6. korekce chyby hodin měřením na místě se známou polohou
   7. určení polohy a chyby hodin pomocí zatmění a zákrytů (velmi vzácné)
   8. korekce chyby hodin pomocí galileovských měsíců Jupitera (obtížně použitelné)

V dalším textu si řekneme více o metodách, které jsme heslovitě sepsali výše.

Zeměpisná šířka z průchodu nebeského tělesa meridiánem

Klasický způsob určení zeměpisné šířky s tisíciletou historií. Potřebujeme pouze změřit výšku tělesa nad obzorem v okamžiku kulminace a znát jeho aktuální deklinaci.
Nejčastěji používaným tělesem je Slunce, pak tuto metodu nazýváme metodou pravého poledne. Nevýhodou Slunce je, že se jeho deklinace neustále mění, nejrychleji kolem rovnodenností, kdy se deklinace během 24 hodin změní o více než 20 úhlových minut, nejpomaleji kolem slunovratů, kdy zůstává několik dní prakticky stejná.
Výšku hvězd a planet můžeme měřit většinou jen během nautického úsvitu a soumraku, což je pro tuto metodu činí obtížně použitelné.
Za určitých podmínek by mělo být možné použít kulminaci Měsíce, prakticky nevyzkoušeno.

Průchod nebeského tělesa nadhlavníkem

Metoda známá hlavně z polynézské navigace. Je použitelná kdykoli během noci, nevyžaduje sextant. Extrémně jednoduchá na výpočet – při průchodu hvězdy nadhlavníkem je zeměpisná šířka pozorovatele rovna deklinaci hvězdy.
Jak poznat, že je hvězda přímo v nadhlavníku? To je na samostatný článek 🙂

Měření Polárky s odhadem korekce Q

Polárka opisuje kružnici kolem severního magnetického pólu o poloměru zhruba půl úhlového stupně. Pokud chceme změřit zeměpisnou šířku pomocí polárky, musíme aplikovat korekci Q, která představuje úhlovou vzdálenost Polárky od pólu v dany okamžik. Nemáme-li přesný čas, můžeme korekci odhadnout pomocí aktuální pozice cirkumpolárních souhvězdí (Velký vůz, Kasiopea). Výbornou pomůzkou je třeba tento diagram , který vytvořil Greg Rudzinski.

Tři výše uvedené metody fungují i když nemáme žádný zdroj času. Následující metody vyžadují, abychom měli možnost měřit časové intervaly (stopky, hodinky, které neukazují přesný čas) Nepotřebujeme mít čas synchronizovaný s UTC ani znát aktuální odchylku.

Kontrola zeměpisné šířky metodou stejných výšek

Velmi elegantní metoda, kterou můžeme použít, když se nám nepodaří určit výšku objektu metodou pravého poledne. Což se na oceánu, i v tropických šířkách, stává překvapivě často.
Potřebujeme změřit, kolik času uplyne mezi dvěma okamžiky, kdy je nebeský objekt (typicky Slunce) ve stejné výšce před kulminací a po kulminaci.
Pak si položíme otázku: jsme severněji, nebo jižněji, než určitá zeměpisná šířka L?
Zeměpisnou šířku, kterou kontrolujeme, dosadíme do vzorce

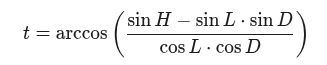
kde H je změřená výška objektu a D jeho deklinace.
Hodnota t je lokální hodinový úhel objektu (LHA) na zeměpisné šířce L.
LHA představuje úhel mezi objektem a lokálním meridiánem, proto když tuto hodnotu vynásobíme dvěma

dostaneme úhel, o který se Země otočí za dobu, kdy bude objekt ve stejné výšce při cestě nahoru a při cestě dolů.
Tuto hodnotu můžeme přímo přepočítat na čas v hodinách

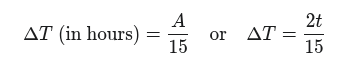
a porovnat s časem, který jsme naměřili my. Pokud je vypočítaný čas kratší, než naměřený, znamená to, že jsme severněji než kontrolovaná šířka. Pokud je čas vypočítaný čas delší než naměřený, jsme jižněji. Toto platí, pokud je deklinace a kontrolovaná šířka na stejné polokouli (léto), v zimě to bude samozřejmě naopak.

Iterativní určení zeměpisné šířky

Výše uvedený postup můžeme opakovat pro různé zeměpisné šířky a iterativně tak zjistit skutečnou zeměpisnou šířku, na které se nacházíme.
Pokud použijeme třeba metodu půlení intervalu, tak začneme-li se šířkou, která se od naší skutečné liší o 3 stupně, během pěti iterací se dostaneme na přesnost lepší než 10 mil.

Kontrola zeměpisné šířky ze dvou libovolných měření

Metodu stejných výšek můžeme samozřejmě použít, i když naměřené výšky nejsou stejné, jen se nám zdvojnásobí množství výpočtů, protože místo jednoho výpočtu LHA a vynásobení dvěma musíme vypočítat LHA dvakrát a úhly od sebe odečíst.
Další postup je stejný, včetně možnosti iterativního určení skutečné zeměpisné šířky.

Určení polohy metodou lunárních vzdáleností

Metoda lunárních vzdáleností byla královskou astronavigační disciplínou v krátkém časovém období mezi vynálezem sextantu (cca 1760) a nasazením použitelných chronometrů (1770). Umožňuje získat jak zeměpisnou šířku, tak zeměpisnou délku. Pro úspěšné použití metody potřebujeme provést minimálně čtyři měření:

1. získat lokální sluneční čas metodou pravého poledne
2. změřit výšku měsíce
3. změřit výšku tělesa, jehož lunární vzdálenost budeme počítat
4. změřit lunární vzdálenost

Poslední tři měření musí proběhnout velice rychle po sobě.
Metoda je velice náročná na přesnost měření (zejména lunární vzdálenosti), vyžaduje rozsáhlé tabulky a více výpočtů, než jiné metody.
Nautical Almanac publikuje tabulky potřebné pro výpočty: https://thenauticalalmanac.com/Lunar_Distance_Tables.html
Stručný (ale dostačující) popis metody je například zde: https://reednavigation.com/easylunars/
Metodou lunárních vzdáleností jsme schopni určit zeměpisnou délku a můžeme tudíž podle ní korigovat čas našich hodin.

Iterativní zjištení chyby hodin metodou lunární výšky

Pokud máme funkční hodiny, jen nevíme, jakou odchylku vůči UTC zrovna mají, můžeme se pokusit tuto odchylku zjistit pomocí měření výšky měsíce. Postupujeme tak, že rychle za sebou změříme výšku dvou nebeských objektů (nejlépe hvězdy) a výšku Měsíce. Pro praktické použití je potřeba, aby byl Měsíc co nejvíce na východě nebo na západě.
V dalším kroku budeme předpokládat, že náš čas na hodinkách je správný a vypočítáme a vykreslíme tři poziční linie, které z měření získáme.
Poziční linie se nám neprotnou v bodě, ale vytvoří trojúhelník, protože poziční linie Měsíce bude díky jeho rychlému pohybu po obloze zatížena chybou odpovídající odchylce našich hodinek od UTC. Upravíme čas, znovu vypočteme poziční linie a takto postupujeme, dokud nezískáme odchylku hodinek s požadovanou přesností.
Celý postup je podrobně popsán zde
Variantou, která je potenciálně výpočetně jednodušší (její funkčnost nebyla zatím ověřena) je změřit dvakrát během dne výšku Slunce a Měsíce, vypočítat dvě sady pozičních linií a odchylku hodinek určit jako rozdíl v zeměpisné délce mezi průsečíky těchto sad pozičních linií. Postup je popsán zde

Korekce chyby hodin měřením na místě se známou polohou

Pokud jsme na místě, jehož geografické souřadnice známe, můžeme zjistit chybu našich hodin vcelku jednoduše. Pokusíme se odhadnout přesný čas (UTC) a provedeme sadu měření. Odhadnutý čas přitom použijeme jako by byl skutečný. Poziční linie našich měření se protnou v bodě, který bude odlišný od pozice, na které se nacházíme. Odchylka v zeměpisné šířce by měla být minimální (je to kontrola našeho měření), odchylka v délce je přímo úměrná rozdílu mezi odhadnutým časem a časem skutečným – 4 časové minuty na každou zeměpisnou minutu délky, pokud nám průsečík pozičních linií vyšel na západ od naší skutečné polohy, náš odhadnutý čas se předbíhá, pokud na východ, zpožďuje se.




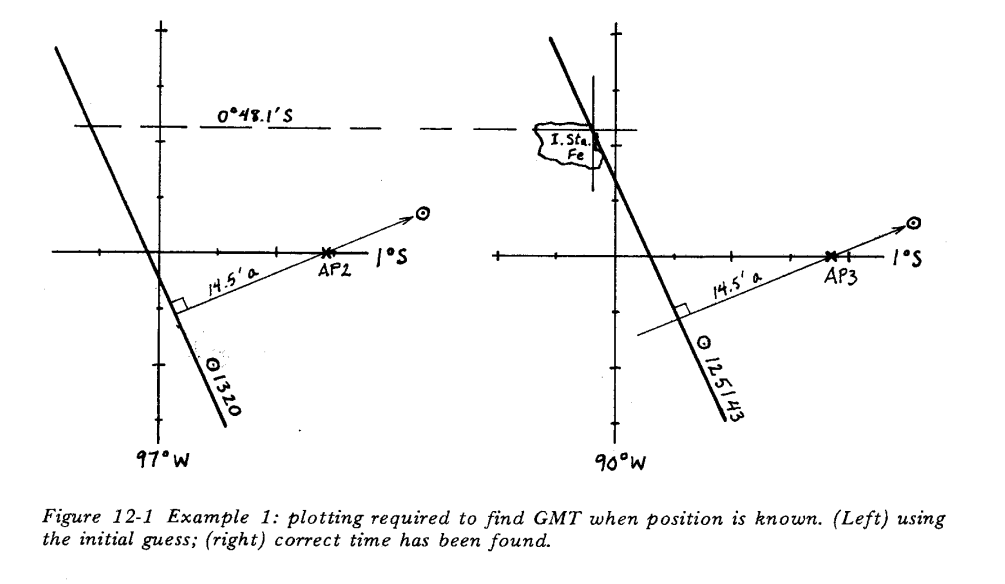
Příklad korekce hodin ze skvělé knihy Celestial Navigation with HO208 od Johna Letchera

Určení polohy a chyby hodin pomocí zatmění a zákrytů (velmi vzácné)

Byla-li by Země dostatečně malá, zatmění Slunce a Měsíce či zákryty planet a jiných nebeských objektů Sluncem či Měsicem by nastávaly kdekoli na Zemi ve stejném okamžiku a pokud bychom čas, kdy nastanou, odpočítali od lokálního pravého poledne (LAN), získali bychom velmi jednoduše naši zeměpisnou délku, a tudíž i čas UTC.
V praxi je ovšem vliv paralaxy poměrně velký. To však problém jen činí složitějším, ne nemožným. Iterativním procesem lze takto zeměpisnou délku určit, ale vzácnost zatmění a zákrytů a výpočetní náročnost znamenají, žr pokud chceme označit nějakou astronavigační metodu za zajímavou, ale velmi okrajovou, bude to zřejmě tato.

Korekce chyby hodin pomocí galileovských měsíců Jupitera (obtížně použitelné)

Oběžné dráhy galileovských měsíců Jupitera (Io, Europa, Ganymed a Callisto) mají jen malý sklon vůči rovině ekliptiky a z pohledu ze Země (stačí k tomu silnější triedr) leží téměř v jedné čáře, procházející rovníkem Jupitera.
Jejich krátké doby oběhu (desítky až stovky hodin) znamenají, že se dají použít jako ciferník k určení přesného času. Na pevné zemi byly s úspěchem používány pro měření zeměpisné délky, na moři se však tato metoda nikdy neprosadila. Možná je na čase se k ní vrátit za použití moderních technologií a zjistit, zda nenastala chvíle pro její renesanci.